论文阅读:LiNeS Post-Training Layer Scaling Prevents Forgetting and Enhances Model Merging
Introduction
Model Merging: Combine avaliable checkpoints, avoiding the costly process of joint trade-offs, such as the forgetting of previously acquired knowledge. However, merging checkpoints fine-tuned on different tasks can lead to significant performance degradation.
Catastrophic Forgetting Mitigation: Many works propose:
- Regularizing the fine-tuning process
- Leveraging the insight that shallow layers capture generalizable representations, and applying lower learning rate to the shallow layers.
However, modifying the fine-tuning process can be complex and computationally expensive. Model editing and model merging methods that directly edit the checkpoints in the weight space.
Drawbacks of Existing Methods: Most model merging methods overlook the insight that shallow layers should remain close to their pre-trained weights to avoid losing the general representations they encode.
Contribution of This Work:
- We propose LiNeS, a post-training editing technique that preserves the zero-shot generalization of pre-trained models while retaining fine-tuned knowledge by applying layer-wise scaling on parameter updates.
- LiNeS significantly enhances multi-task model merging baselines.
- LiNeS can be applied to enhance existing weight interpolation methods.
Wight Interpolation 是 Model Merge 的一种技术/方法。
Related Work
Representation Collapse and Regularized Fine-Tuning:
- Pre-trained models exhibit strong zero-shot performance across diverse data distribution due to the robust and transferable feature representations learned during pre-training.
Feature representation:深度学习模型一般不会直接处理原始数据,而是通过一系列计算将原始数据转换为利于理解的内部表示(Feature Representation)。
- However, fine-tuning on specific tasks often harms the zero-shot generalization performance on distributions different from the fine-tuning domain. This degradation arises from the distortion of pre-trained feature during fine-tuning. A phenomenon referred to as representation collapse.
- Modifying the fine-tuning process is far more computationally expensive compared to post-training merging methods.
Weight Interpolation and Model Merging:
- It is shown that two solutions derived from separate training runs can be connected by nonlinear paths of low loss. Linear mode connectivity extended the paths to the linear case.
原本我们以为从通过不同的起点(随机初始化)出发,最终到达的两个模型(解)是相互隔离的。但是事实上存在一条 loss 很小的路径连接这两个解。
- These insights enabled the transfer of the benefits regarding robustness output ensembles to weight ensembles.
Output Ensembles:把同个问题分别询问多个模型,综合它们的答案来得到最终结果
Weight Ensembles:不再需要保留多个模型,而是直接合并成一个模型
- These findings can be leveraged to improve performance on single-task, out-of-distribution, multi-task and multi-objective alignment settings.
单个任务上训练多个模型合并起来能得到更好的模型,多个任务合并起来能获得多任务的模型。
- Several methods have tried to merge by preserving the important parameters defined via the Fisher Information Matrix, heuristics…
如何合并呢:简单加权肯定不行,因为有时候会直接抵消一些特征。因此有很多改进方法,例如 Fisher Information Matrix、Heuristics 启发式算法等
- Recent works use gradient descent to learn the layer-specific merging coefficients per task, e.g., Ada-merging.
学习如何合并,每一层、每个任务都学习一个独特的合并系数
Post-Training Layer-Wise Scaling Mitigates Forgetting
We present the key insight of this work: Scaling down the updates of shallow layer after fine-tuning can mitigate catastrophic forgetting, restore zero-shot generalization, preserving performance on the target task.
Notation: We consider a pre-trained model $\theta_0 \in \mathbb{R}^N$. Fine-tuning on a specific task $t$ results in the fine-tuned weights $\theta_t$. The task vector or residual for task $t$ is defined as
$$ \tau_t:= \theta_t - \theta_0. $$
Fine-Tuning Leads to Catastrophic Forgetting: Consider an $8$-task image classification problem. We fine-tune a CLIP ViT-B/32 model on each task, measuring performance on the fine-tuned task (target task) and the remaining $7$ tasks (control tasks).
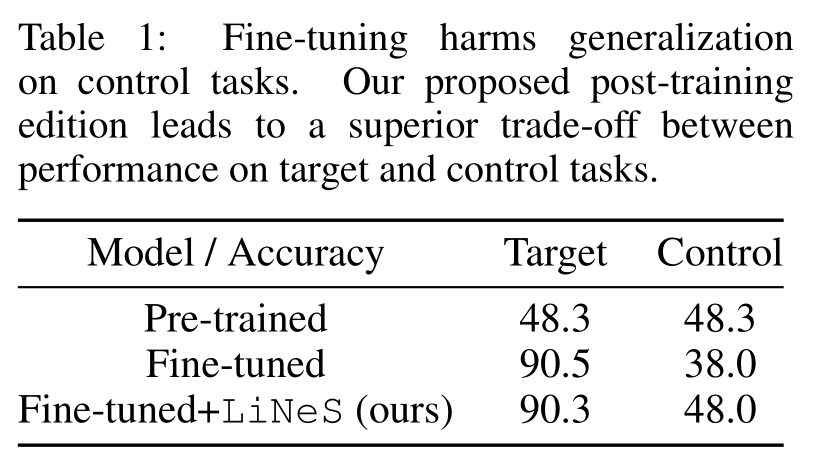
Shallow-Layer Updates Impact Minimally on Target Task Accuracy:
- Most parameter updates during fine-tuning are redundant, as similar performance is achievable without updating most pre-trained weights.
- Prior work shows that task-specific features are often concentrated in deeper layers of the network.
- We apply a scaling factor to the updates to the $\ell$-th layer $\tau^{(\ell)}$,
$$ \lambda^{(\ell)}=\gamma+(1-\gamma)\frac{\ell-1}{L-1}, \quad \forall\ell\in[L],\gamma\in[0,1] $$
- We observe that even with strong downscaling of shallow layers, the target task accuracy remains nearly unaffected. In contrast, when we downscale the deeper layers, target task accuracy drops significantly.
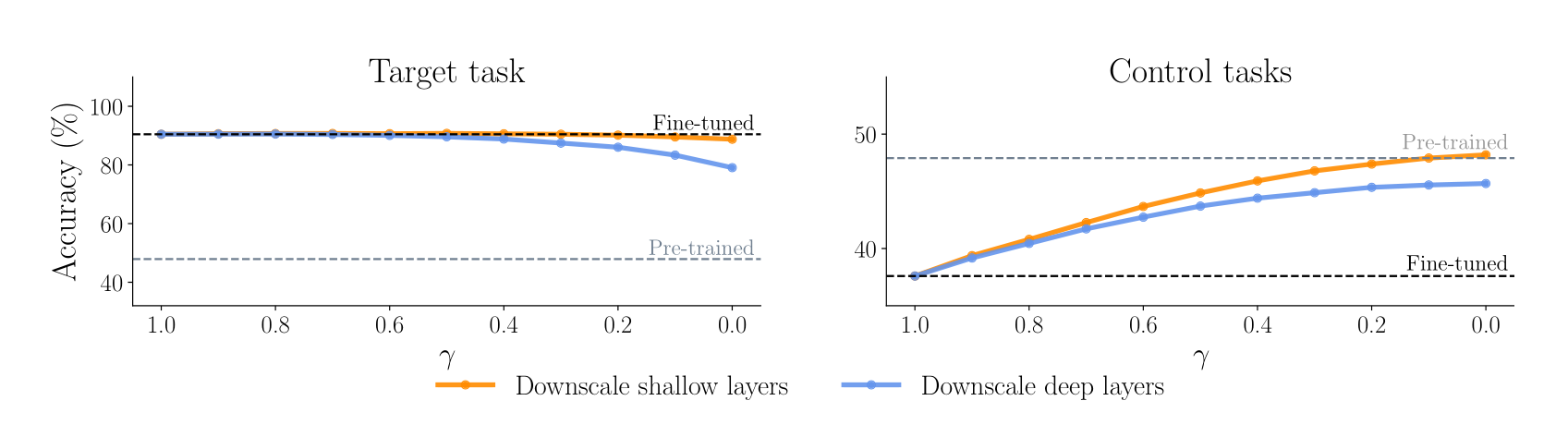
首先进行 Fine-Tune 获得各个层的更新量,然后用 $\lambda^{(\ell)}$ 对各层的更新量进行放缩,$\gamma$ 越小说明浅层更新量被缩小得越厉害。左图中可以看出浅层更新量的改变几乎不影响 Target Task。
Shallow-Layer Updates Undermine Zero-Shot Generalization: We further hypothesize that the degradation of performance on control tasks is largely due to distortions in the shallow layers. We can see that as the strength of the shallow-layer downscaling increases, the accuracy on control tasks approaches the original pre-trained model’s performance.
Improved Trade-Off between Target and Control Performance: We apply the method to a 20-task computer vision benchmark. Figure 2 shows that fine-tuning degrades zero-shot generalization, and our method improves generalization while maintaining near-full target task accuracy.
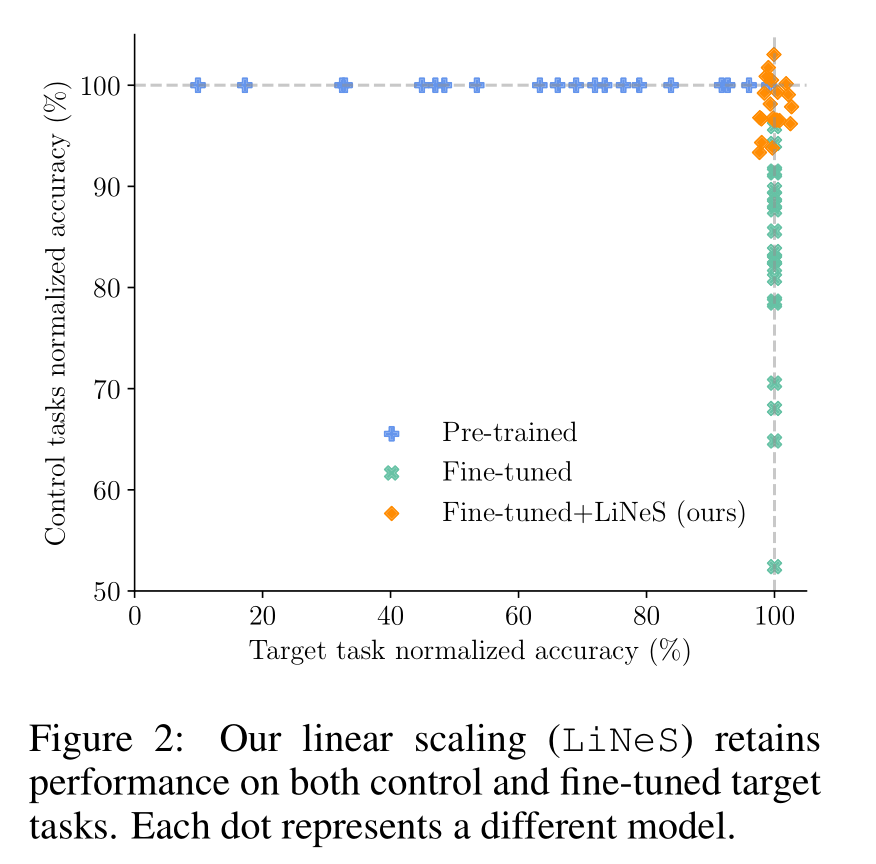
上图中的每个点分别对应 20 个任务。
Method
Layer-increasing Network Scaling: Given a task vector $\tau$ with $L$ layer blocks, we apply layer-wise linear scaling to adjust the contributions of shallow and deep layers using:
$$ \tau_{\mathrm{LiNeS}}=\mathrm{concat}\left(\lambda^{(1)}\tau^{(1)},\ldots,\lambda^{(L)}\tau^{(L)}\right),\quad\mathrm{where} \quad \lambda^{(\ell)}=\alpha+\beta\frac{\ell-1}{L-1},\quad\forall\ell\in[L]. $$
Application in Model Merging: Notice that $\tau$ can correspond to either a single-task residual or, in the context of model merging, a multi-task vector obtained by merging the residuals of multiple checkpoints fine-tuned starting from a common initialization.
Experiments
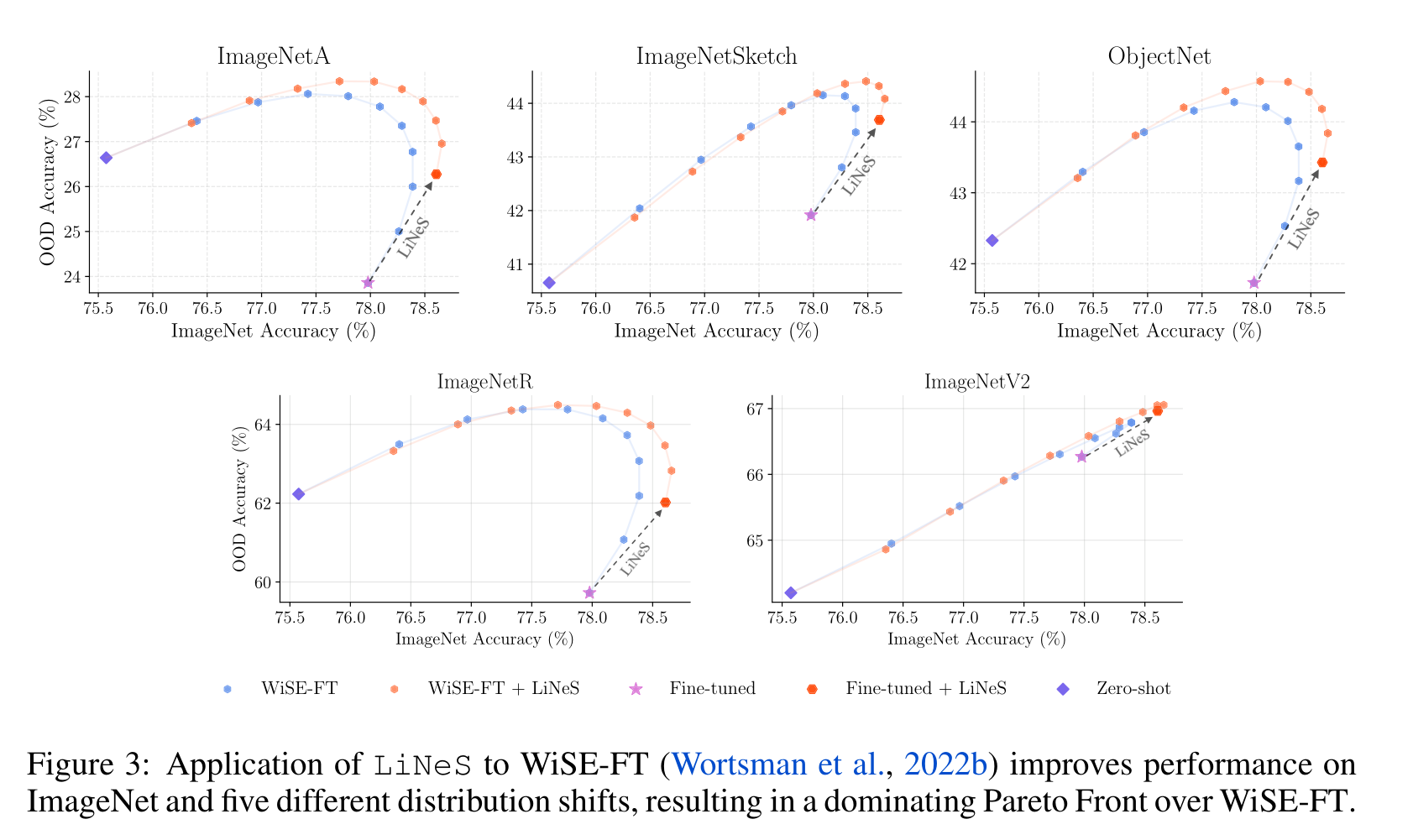
Improving Robust Fine-Tuning for OOD Generalization:
- WiSE-FT: Linearly interpolate between the pre-trained and the fine-tuned weights: $\tau: (1 - \gamma) \theta_0 + \gamma \theta = \theta_0 + \gamma \tau$ for $\gamma \in [0, 1]$.
- We evaluate CLIP models fine-tuned on ImageNet, considering $5$ OOD datasets.
Improving Multi-Task Model Merging:
- Task Arithmetic: Generate a multi-task vector $\tau_{\text{MTL}} = g(\tau_1, \cdots, \tau_T)$ with merging function $g$, and construct $\theta = \theta_0 + \lambda \cdot \tau_{\text{MTL}}$. In this work, “task arithmetic” is implemented by averaging the task vectors.
Task vector 指的是在某个 task 微调后,参数的变化量。
Performance Loss during Merging: This performance decrease partially stems from interference among task vectors.
We can edit each task vector with
LiNeS before merging to restore the generalization to other tasks, or simply edit the merged multi-task vector to preserve the shallow and general features.We tune $\beta$ and set $\alpha$ to
$$ \alpha=\frac{1}{N_{\mathrm{models}}}\frac{\|\tau_{\mathrm{sum}}\|}{\|\tau_{\mathrm{MTL}}\|},\quad \mathrm{where} \quad \tau_{\mathrm{sum}}=\sum_{i=1}^{N_{\mathrm{models}}}\tau_{i} $$
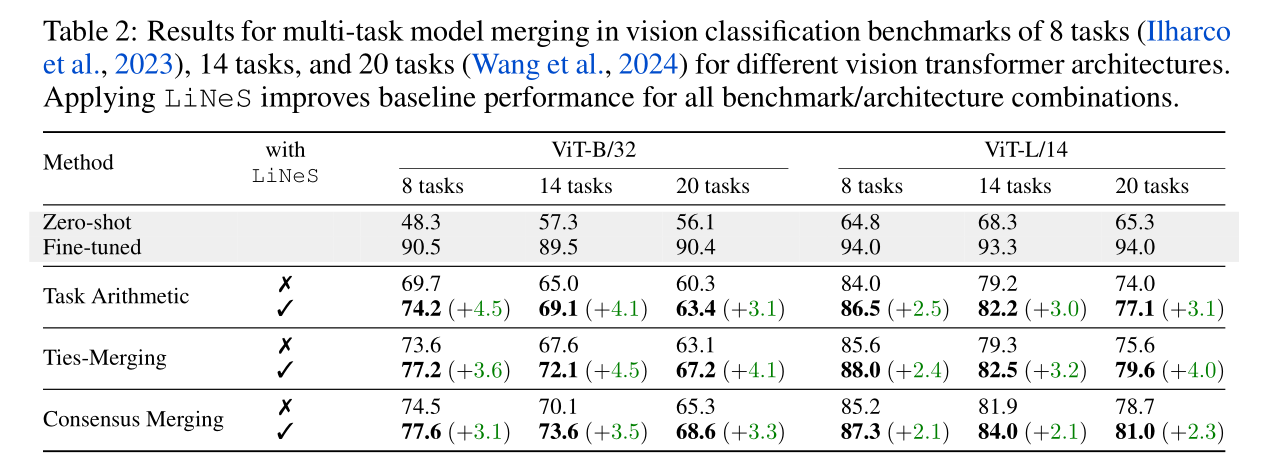
Computer Vision:
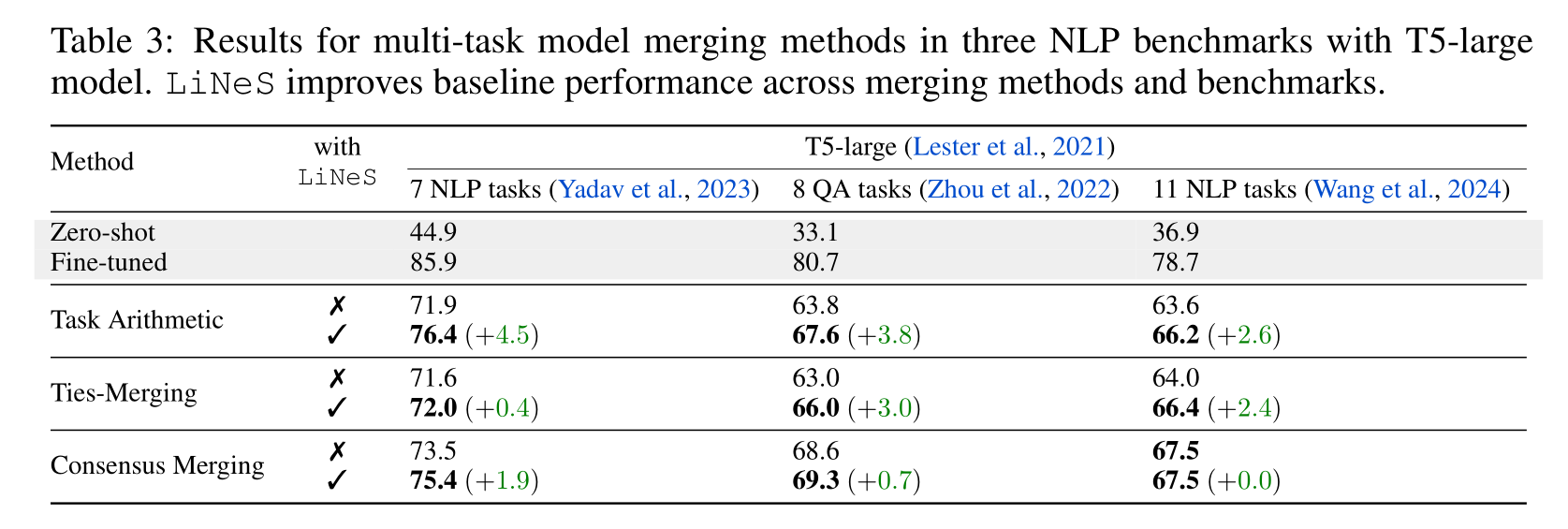
Natural Language Processing:
Model Soups for Merging Single-Task Models: Averaging in weight space multiple models fine-tuned on the same task derived from the same pre-trained model has been shown to increase target performance. We investigate whether LiNeS can enhance the test performance when merging single-task models.
$$ \theta_{\mathrm{soup}}=\theta_0+\tau_{\mathrm{soup}}, \quad \mathrm{where} \quad \tau_{\mathrm{soup}}=\frac{1}{N_{\mathrm{models}}}\sum_{i=1}^{N_{\mathrm{models}}}\left(\boldsymbol{\theta}_i-\boldsymbol{\theta}_0\right) $$
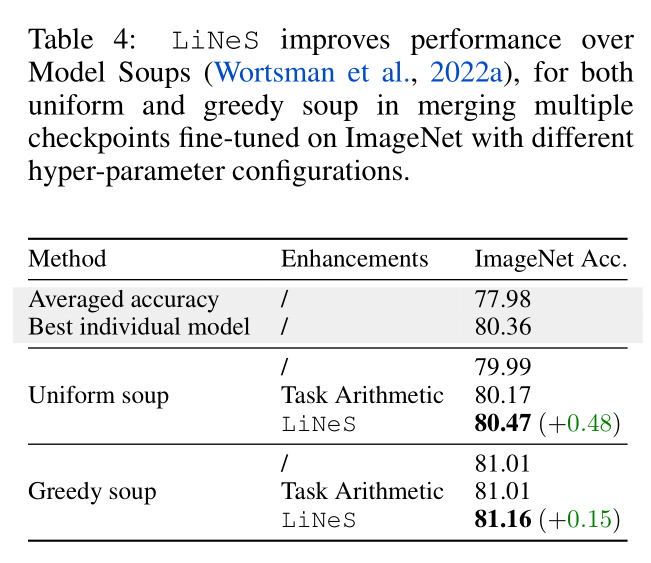
Uniform Soup 指把所有模型平等看待,Greedy Soup 表示保留一个验证集对模型进行筛选
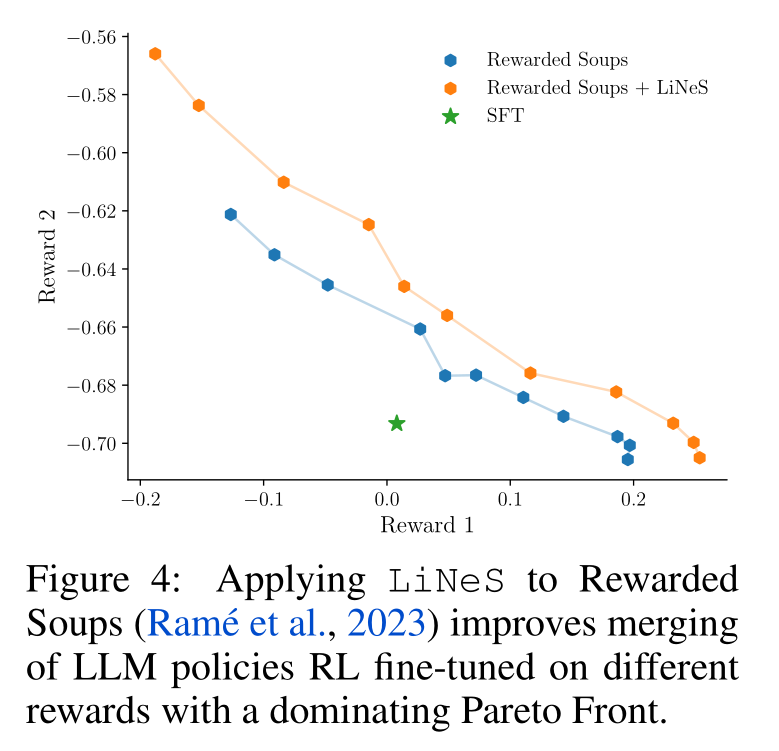
Improving Rewarded Soups:
- Starting with an LLM parameterized by weights $\theta_0$, we first fine-tune it using SFT resulting in weights $\theta_{\text{SFT}}$.
- We then apply RLHF, training two independent policies via PPO to maximize the rewards $R_1$ and $R_2$.
- We linearly interpolate the residuals $\tau_1 = \theta_1 - \theta_{\text{SFT}}$ and $\tau_2 = \theta_2 - \theta_{\text{SFT}}$
$$ \theta_{RS}=\theta_{\mathrm{SFT}}+\lambda\tau_{1}+(1-\lambda)\tau_{2},\quad\lambda\in[0,1], $$
Discussion
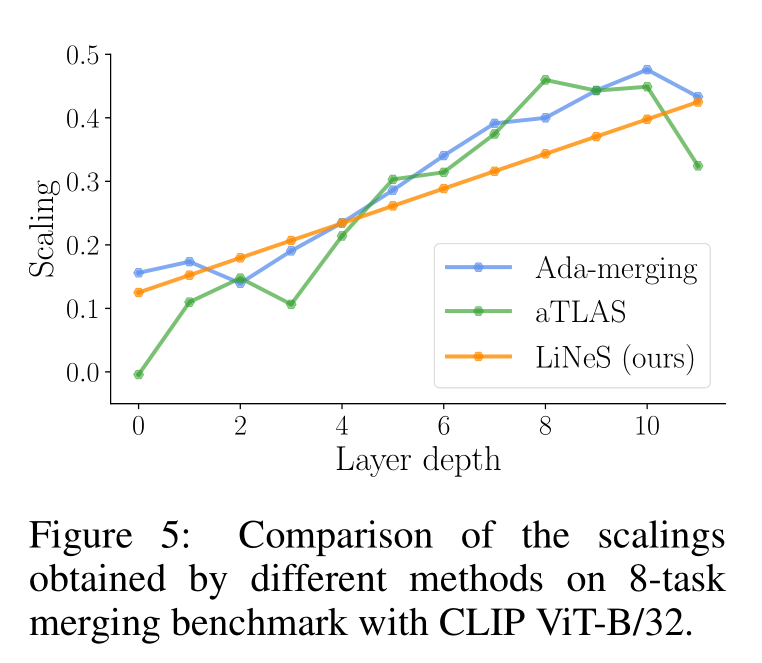
We compare LiNeS with prior work that optimizes the scaling coefficients via backpropagation:
- Ada-Merging: Minimizes the entropy loss of the predictions on the test set
- aTLAS: Minimizes a cross entropy loss on validation samples
Both methods operate on a more fine-grained level and introduce coefficients per layer and per task. Ada-merging and aTLAS requires excessive memory overhead and multiple training epochs.
Questions and Comments
- 模型合并和缓解遗忘很像:无非就是解决任务/数据的冲突
- Layer-Wise:线性的 scaling 一定是最优的吗?能不能有更好的方式?
- Task-Wise:不同任务之间能不能更好的合并方式?
- Catastrophic Forgetting:Representation Learning 中有没有其他相关的结论,能直接拿来用?