论文阅读:Parameter-Efficient Fine-Tuning with Controls
Introduction
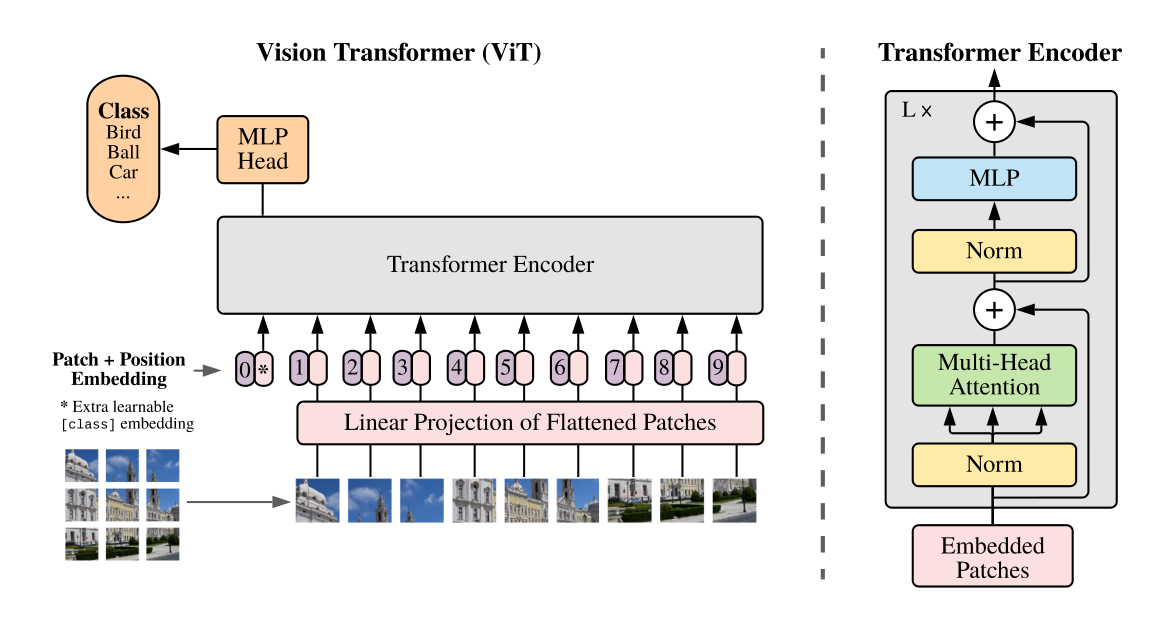
ViT:
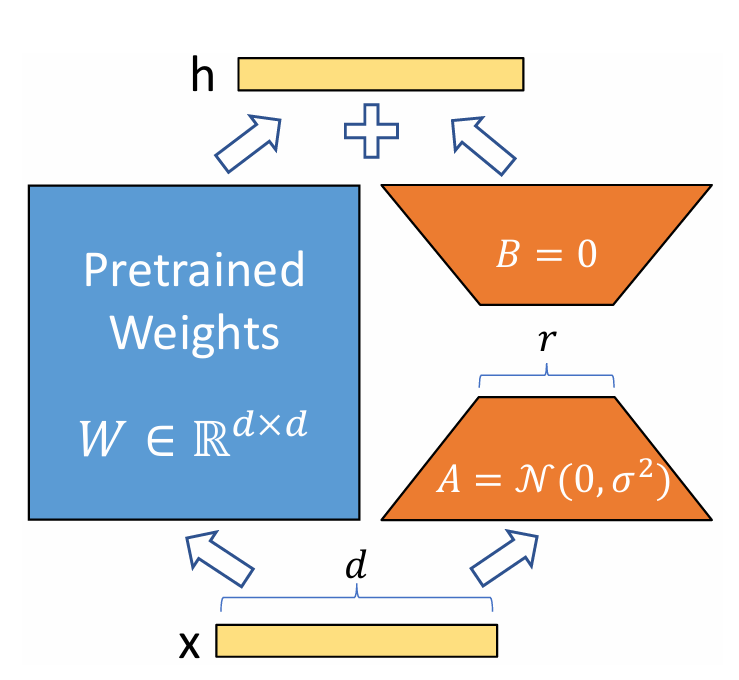
LoRA: LoRA (Low-Rank Adaptation) freezes the original model weights and injects trainable, low-rank matrices into its layers.
AdaptFormer: AdaptFormer adapts Vision Transformers to new tasks by inserting small, lightweight modules in parallel to the existing feed-forward networks.
A Control Formulation of PEFT Algorithms
Notation: Given an image $x_0 \in \mathbb{R}^{C \times H \times W}$(Channel, Height, Width), the ViT model splits and embeds it into visual tokens $x_0^\prime \in \mathbb{R}^{m \times d}$, where $m$ denotes the number of tokens and $d$ refers to the length of each token. By adding an additional class-token, ViT forms $x_1 \in \mathbb{R}^{(m+1) \times d}$. The $t$-th block of ViT is defined as:
$$ x_{t+\frac12}=\text{MHSA}(\text{LN}(x_t))+x_t, \quad x_{t+1}=\text{FFN}(\text{LN}(x_{t+\frac12}))+x_{t+\frac12} $$
for $t = 1,2, \cdots, T-1$. Here MHSA, FFN and LN denote the multi-head self-attention, feed-forward network and layer normalization, respectively.
Dynamics of LoRA: LoRA finds functions $\{g_t\}$ to
$$ x_{t+1}=f_{t}\left(x_{t},\theta_{t},g_{t}(x_{t},u_{t})\right). $$
where $x_t \in \mathbb{R}^{(m+1) \times d}$ is the token at the $t$-th layer, $\theta_t$ is the parameter at the $t$-th layer, and $g_t(x_t, u_t) = x_tu_t$ satisfies
$$ u_t=A_tB_t,\quad A_t\in\mathbb{R}^{d\times r},B_t\in\mathbb{R}^{r\times d}, \quad r\ll d. $$
Dynamics of AdaptFormer: The dynamics can be expressed as
$$ x_{t+1}=f_t(x_t,\theta_t)+g_t(x_t,u_t). $$
Overall Goal: The objective is to find the control such that the terminal loss on downstream tasks could be minimized:
$$ \min_{\{u_t,\theta_T\}}\frac1N\sum_{i=1}^N\mathcal{L}(x_{\mathrm{Pred},i},y_i) $$
such that
$$ x_{t+1,i}={f}_t(x_{t,i},\theta_t)+g_t(x_{t,i},u_t), \quad t\in[1,\cdots,T-1], $$
$$ x_{\mathrm{Pred},i}=f_T(x_{T,i}^\mathrm{cls},\theta_T). $$
Here $N$ indicates the number of samples.
Controllability Analysis
A Sufficient Condition for Controllability:

Benefits of Nonlinear Controller: Let $N$ denote the number of samples and $D$ denotes the dimension of state/parameter.
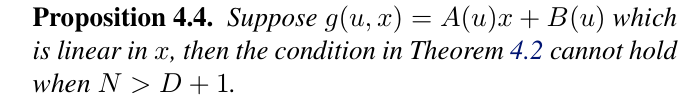
Nonlinear Controller Design
CPA (Cross-Patch Attention) : Add additional cross-patch mechanism
$$ x^{p(j’)}=\text{CPA}(x)=\sum_j\frac{\exp\langle x^{p(i)},x^{p(j)}\rangle}{\sum_m\exp\langle x^{p(i)},x^{p(m)}\rangle}x^{p(j)} $$
where $x^{p(j)}$ denotes the $j$-th patch of $x$.
Nonlinear Controller Design:
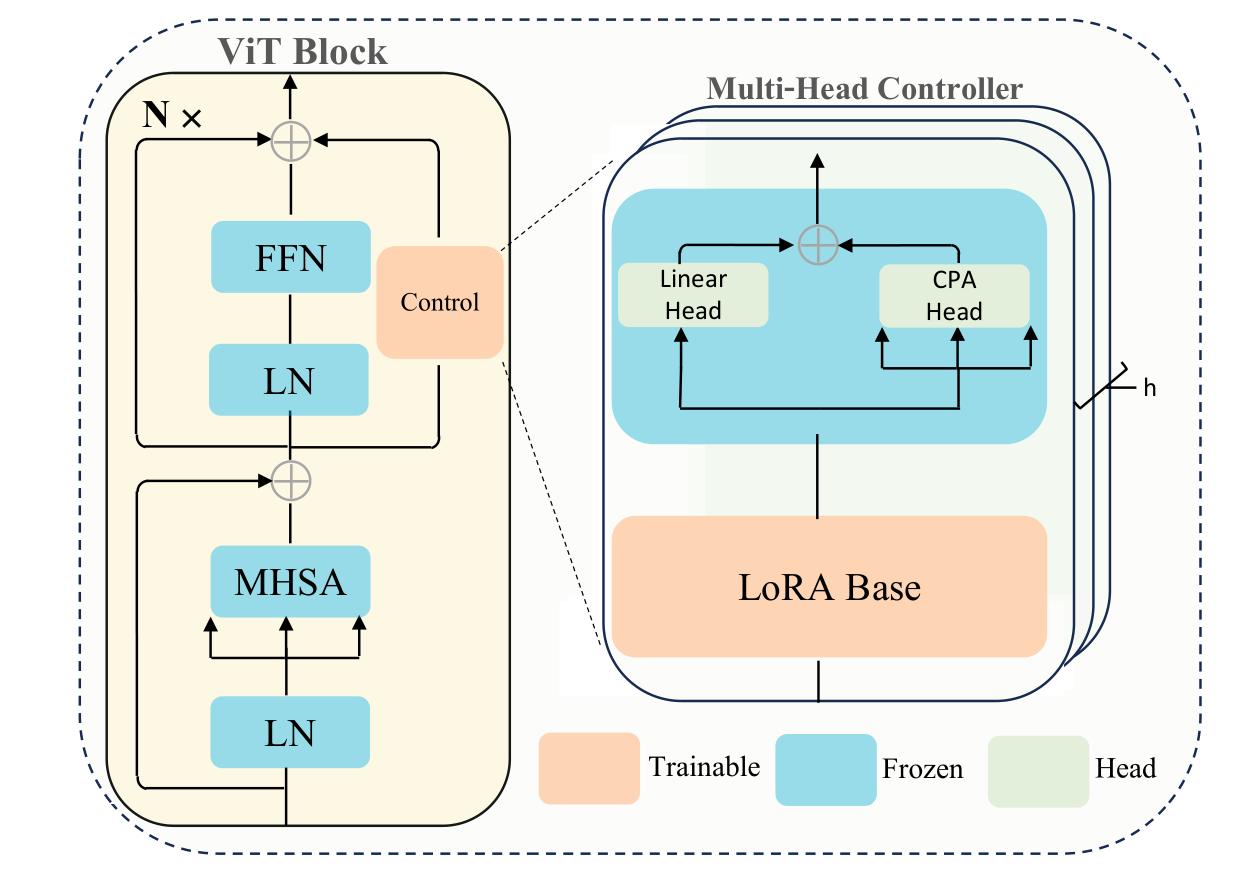
$$ \operatorname{Control}(x)=\operatorname{LoRA}(x)+\operatorname{CPA}\left(\operatorname{LoRA}(x)\right) $$
Experiments
Competing Algorithms: We compare our method with the following algorithms:
- Full-Tuning
- Linear Probing: Appending an additional trainable linear layer on top of the pre-trained model while keeping the rest parameters fixed.
- Visual Prompt Tuning (VPT): Concatenating a set of trainable tokens with existing image tokens.
- LoRA: Injecting trainable low-rank matrices to $W_Q$ and $W_V$.
- AdaptFormer: A vision-specific LoRA algorithm by perturbing the FFN layer with (almost) linear controls.
Experiments on Vision Benchmarks:
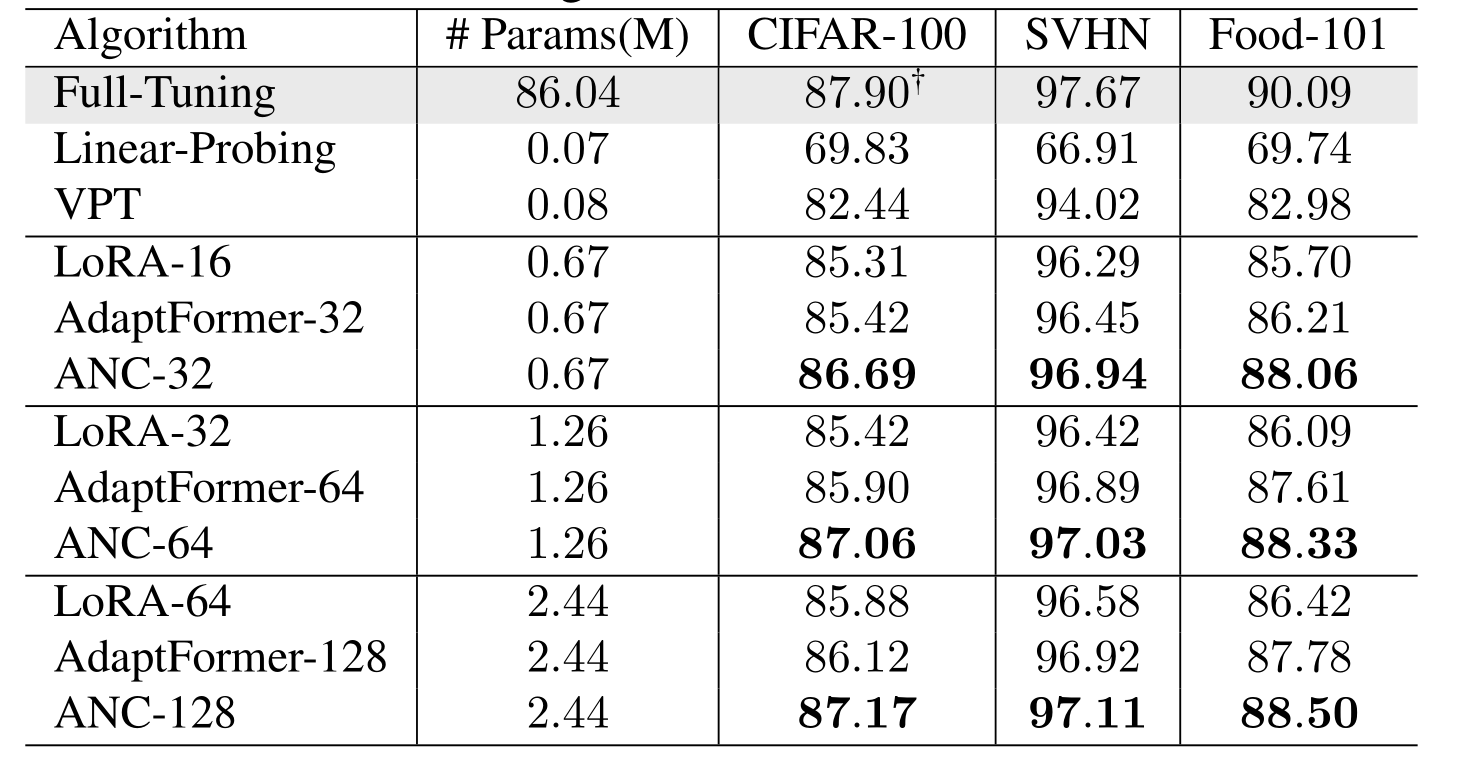
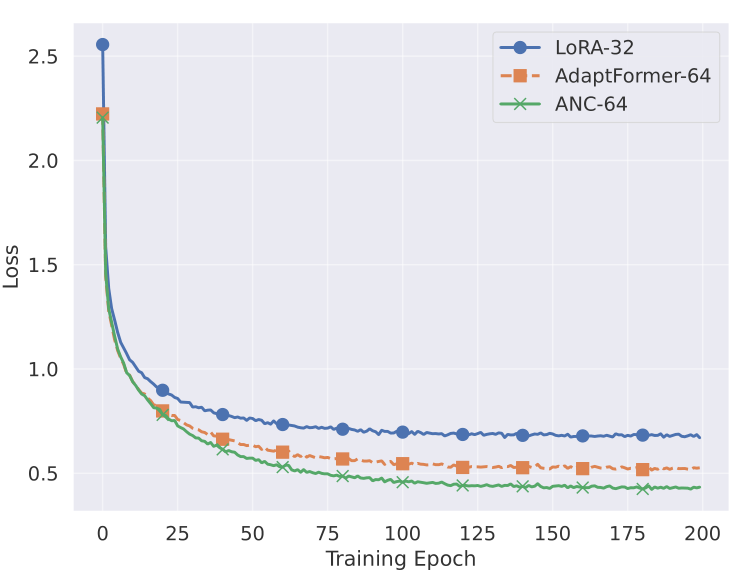
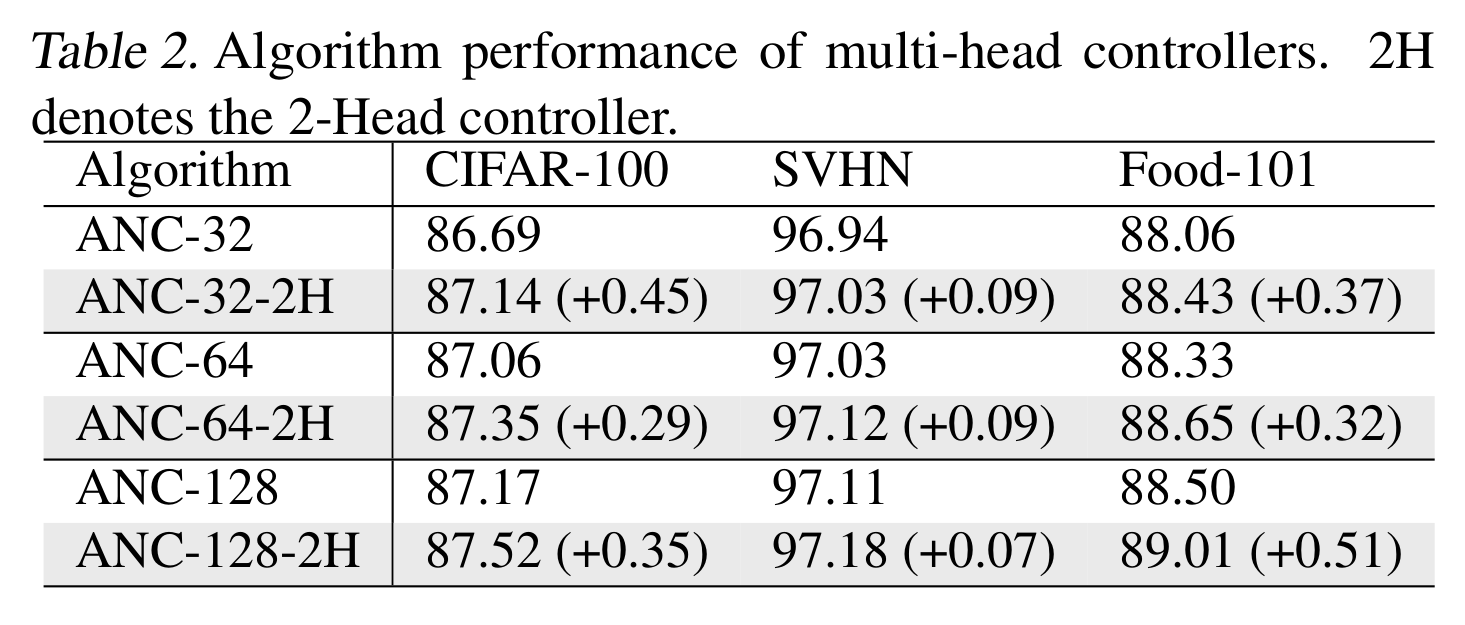
Multi-Head Controller Experiment: