神经正切核 Neural Tangent Kernel, NTK
在文章 [2407.10490] Learning Dynamics of LLM Finetuning 中我们接触到了神经正切核的概念,其刻画了不同数据对参数、Logits 的影响。
问题回顾
分类问题:我们考虑多分类问题,将输入 $\mathbf{x}$ 映射至 $\mathbf{y} \in \mathcal{V}$,其中 $\mathcal{V}$ 是大小为 $V$ 的字典。模型会先输出 logits $\mathbf{z} = h_\theta(\mathbf{x}) \in \mathbb{R}^V$,然后取 Softmax:
$$ \mathbf{x} \xrightarrow{\text{Hidden Layers}} \underbrace{ \mathbf{z} = h_{\theta}(\mathbf{x}) = \begin{bmatrix} z_1\\ z_2 \\ \vdots \\ z_V \end{bmatrix}}_{\text{logits}} \xrightarrow{\text{Softmax}} \underbrace{ \begin{bmatrix} \pi_{\theta}(y_1\mid \mathbf{x})\\ \pi_{\theta}(y_2\mid \mathbf{x})\\ \vdots\\ \pi_{\theta}(y_V\mid \mathbf{x}) \end{bmatrix}}_{\text{confidence}}. $$
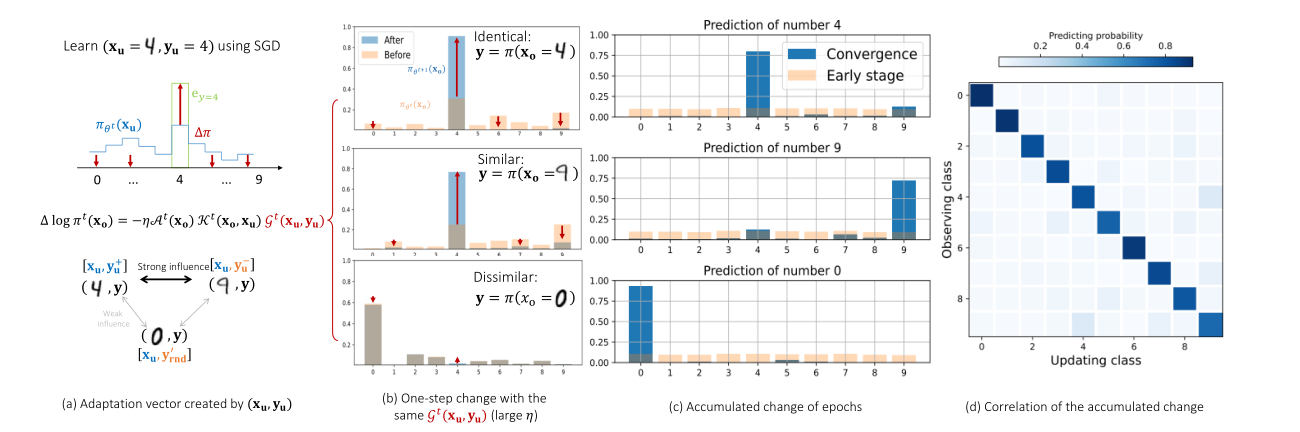
学习样本的 Dynamics:考虑学习新样本 $(\mathbf{x}_u, \mathbf{y}_u)$,学习率为 $\eta$,通过在 $\mathbf{x}_u$ 上进行一次梯度下降,模型在 $\mathbf{x}_o$ 上预测的变化值:
$$ \Delta \log \pi^t(\mathbf{y} \mid \mathbf{x}_o) := \log \pi_{\theta^{t+1}}(\mathbf{y} \mid \mathbf{x}_o) - \log \pi _{\theta^t}(\mathbf{y} \mid \mathbf{x}_o). $$
Learning Dynamics:单步的 Learning Dynamics 为
$$ \underbrace{\Delta \log \pi^t(\mathbf{y} \mid \mathbf{x}_o)}_{V \times 1} = -\eta \underbrace{\mathcal{A}^t(\mathbf{x}_o)}_{V \times V} \underbrace{\mathcal{K}^t(\mathbf{x}_o, \mathbf{x}_u)}_{V \times V} \underbrace{\mathcal{G}^t(\mathbf{x}_u, \mathbf{y}_u)}_{V \times 1} + \mathcal{O}\bigl(\eta^2 \|\nabla_\theta \mathbf{z}(\mathbf{x}_u)\|_{\text{op}}^2\bigr), $$
- $\mathcal{A}^t = \nabla_{\mathbf{z}} \log \pi_{\theta^t}(\mathbf{x}_o) = I - \mathbf{1} \pi^{\top}_{\theta^t}(\mathbf{x}_o)$ 将 logits 中的变化 $\Delta \mathbf{z}$ 映射到输出分布 $\log \pi (\mathbf{y} \mid \mathbf{x}_o)$,即对应着 Softmax 的矩阵表达;
- $\mathcal{K}^t(\mathbf{x}_o, \mathbf{x}_u) = (\nabla_{\theta}\mathbf{z}(\mathbf{x}_o)\mid_{\theta^t})(\nabla_{\theta}\mathbf{z}(\mathbf{x}_u)\mid_{\theta^t})^{\top}$ 衡量了 $\mathbf{x}_o$ 和 $\mathbf{x}_u$ 的相互影响程度;
- $\mathcal{G}^t(\mathbf{x}_u, \mathbf{y}_u) = \nabla_{\mathbf{z}}\mathcal{L}(\mathbf{x}_u, \mathbf{y}_u)\mid_{\mathbf{z}^t}$ 从当前分布指向期望的分布,即误差信号。
神经正切核的理解
$\nabla_\theta \mathbf{z}(\mathbf{x})$ 的理解:$\mathbf{z}(\mathbf{x}) \in \mathbb{R}^V$ 是模型对输入 $\mathbf{x}$ 输出的 logits 向量,$\theta \in \mathbb{R}^P$ 是模型所有参数构成的向量,因此 $\nabla_\theta \mathbf{z}(\mathbf{x})$ 是 $\mathbf{z}(\mathbf{x})$ 关于 $\theta$ 的 Jacobian Matrix:
$$ \nabla_\theta\mathbf{z}(\mathbf{x})= \begin{bmatrix} \frac{\partial z_1}{\partial\theta_1} & \frac{\partial z_1}{\partial\theta_2} & \ldots & \frac{\partial z_1}{\partial\theta_P} \\ \frac{\partial z_2}{\partial\theta_1} & \frac{\partial z_2}{\partial\theta_2} & \ldots & \frac{\partial z_2}{\partial\theta_P} \\ \vdots & \vdots & \ddots & \vdots \\ \frac{\partial z_V}{\partial\theta_1} & \frac{\partial z_V}{\partial\theta_2} & \ldots & \frac{\partial z_V}{\partial\theta_P} \end{bmatrix}. $$
$\nabla_\theta \mathbf{z}(\mathbf{x})$ 的第 $i$ 行 $\nabla_\theta {z}_i(\mathbf{x})$ 表示了为了使第 $i$ 个 logit $z_i$ 增长得最快,模型 $\theta$ 应该更新的方向。换而言之,模型 $\theta$ 对第 $i$ 个 logit 的敏感度。
矩阵乘积的含义:我们来分析 $\mathcal{K}$ 的第 $(i,j)$ 个元素,其是 $\nabla_\theta z_i(\mathbf{x}_o)$ 与 $\nabla_\theta z_j(\mathbf{x}_u)$ 的内积
$$ \mathcal{K}_{ij}=(\nabla_\theta z_i(\mathbf{x}_o))\cdot(\nabla_\theta z_j(\mathbf{x}_u))^\top=\sum_{p=1}^P\frac{\partial z_i(\mathbf{x}_o)}{\partial\theta_p}\frac{\partial z_j(\mathbf{x}_u)}{\partial\theta_p} $$
- 向量 $\nabla_\theta z_i(\mathbf{x}_o)$ 是在参数空间 $\mathbb{R}^P$ 中,能够最有效提升【输入为 $\mathbf{x}_o$ 时第 $i$ 个类别的 logit 值】的方向;
- 向量 $\nabla_\theta z_j(\mathbf{x}_u)$ 是在参数空间 $\mathbb{R}^P$ 中,能够最有效提升【输入为 $\mathbf{x}_u$ 时第 $j$ 个类别的 logit 值】的方向。
参数空间中的相似性:$\mathcal{K}_{ij}$ 作为一个度量矩阵,其度量了两个方向在参数空间中的对齐程度或一致性
- 若 $\mathcal{K}_{ij}$ 为很大的正数:意味着那些能够有效提升 $z_i(\mathbf{x}_o)$ 的参数更新,同样也有效于提升 $z_j(\mathbf{x}_u)$;
- 若 $\mathcal{K}_{ij}$ 接近于 $0$:两个方向在参数空间正交,改变参数来影响 $z_i(\mathbf{x}_o)$ 对 $z_j(\mathbf{x}_u)$ 几乎没有影响,反之亦然;
- 若 $\mathcal{K}_{ij}$ 为很大的负数:两个方向是相反的,提升 $z_i(\mathbf{x}_o)$ 的参数更新会导致 $z_j(\mathbf{x}_u)$ 的下降。
在 Learning Dynamics 中的作用:$\mathcal{K}^t(\mathbf{x}_o, \mathbf{x}_u)$ 接收来自于 $\mathbf{x}_u$ 的误差信号 $\mathcal{G}^t$,并将其翻译为对 $\mathbf{x}_o$ 的 logits $\mathbf{z}(\mathbf{x}_o)$ 的影响